曲線

[ゲスト]

曲線について、まだやりはじめたばかりなのですが入試問題でも良い基本問題だから、と宿題に出されました。
詳しい説明をしてくださると助かります。

[ゲスト]

（１）
aについて整理すると
\begin{align}
（y^2-2x-3)a+x^2-1=0…①\\
\end{align}
となります。
この式がaによらず成り立つ条件は
\begin{align}
y^2-2x-3=0,x^2-1=0\\
∴x=±1\\
\end{align}
$x=1$のとき$y^2=5,x=-1$のとき$y^2=1$
よって
$(1,\sqrt{5}),(1,-\sqrt{5})(-1,1),(-1,-1)$の4定点を通る。

[ゲスト]

（２）
①で、$y^2-2x-3=0$のときは（１）で求めた4点になるが、
$y^2-2x-3≠0$のとき
\begin{align}
a=\frac{1-x^2}{y^2-2x-3}…②\\
\end{align}
となる。
$a>0$より
\begin{align}
\frac{1-x^2}{y^2-2x-3}>0\\
\end{align}
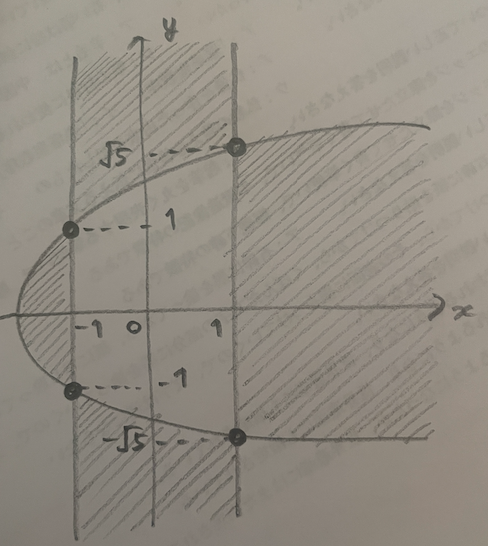
添付した図の示す色がついた部分。境界は黒点のみ含む。